Relationship Between Exterior And Interior Angles Of A Polygon

What Is The Relationship Between The Exterior Angle At A

Aug 18, 2016 explanation: enter image source here. interior angle is formed by two sides of a polygon. the corresponding exterior angle is formed by one of . The interior angles of a polygon are those angles at each vertex that are on the inside of the polygon. there is one per vertex. so for a polygon with n sides, there are n vertices and n interior angles. for a regular polygon, by definition, all the interior angles are the same. in the figure above, click on "make regular" then change the number of sides and resize the polygon by dragging any.

The sum of the measures of the interior angles of a polygon with n sides is (n 2) 180. · the measure of each interior angle of an equiangular n-gon is image2. · if . Interiorangles in polygons displaying top 8 worksheets found for this concept.. some of the worksheets for this concept are 6 polygons and angles, sum of angles in polygons work answer key, polygons quadrilaterals and special parallelograms, sum of polygons, angles in polygon 1, interior angle 1, relationship between exterior and remote interior angles, interior and exterior angles.

Interior And Exterior Angles Worksheet Amazing Ideas

Any angle formed by adjacent sides of a polygon opening inside the polygon is called an interior angle. exterior angle is formed by one side of a polygon and by extending the adjacent side outside the polygon. it will open on the outside of the polygon. interior angle + exterior angle = 180 degrees for any vertex of a polygon. A polygon's exterior angle is not equal to 360 degrees minus the measure of the interior relationship between exterior and interior angles of a polygon angle. a polygon's interior and exterior angles at a given vertex don't span . Interior and exterior angles of a polygon displaying top 8 worksheets found for this concept.. some of the worksheets for this concept are 6 polygons and angles, 4 the exterior angle theorem, name geometry polygons n, polygons quadrilaterals and special parallelograms, interior and exterior angles, mathematics linear 1ma0 angles polygons, relationship between exterior and remote interior.

Internal And Externalangles Wikipedia

Relationships between exterior and interiorangles of polygons relationship an interior angle of a polygon is always supplementary to an exterior angle at its vertex, therefore they would add up to 180 degrees. equation a quick way to find the sum of each interior angle of a. Since you are extending a side of the polygon, that exterior angle must necessarily be supplementary to the polygon's interior angle. together, the adjacent interior . Mar 16, 2016 learn how to find the interior and exterior angles of a polygon in this free math video tutorial by mario's math tutoring. we discuss regular and .

Jul 28 2012 updated. this assemblage of printable angles in polygons worksheets for grade 6 through high school encompasses a multitude of exercises to find the sum of interior angles of both regular and irregular polygons find the measure of each interior and exterior angle simplify algebraic expressions to find the angle measure and much more. Measure of interior and exterior angles ofpolygons. study. flashcards. learn. write. spell. test. play. individual interiorangle. 180(n-2)/n. sum of exteriorangles. 360. sum of an individual exteriorangle. 360/n. explain relationshipbetween the number of sides of a polygon and the number of diagonals. as each exterior angle of a. The exterior angle and an interior angle lie in a straight line so they form an angle whose measure is 180. if the interior angle is 45, then take 180 minus 45 and get 135. if the interior angle is 36, then take 180 minus 36 and get 144. this is true for one angle drawn at that vertex. you can do this for all of the other vertices. The exterior angle is the angle between any side of a shape, and a line extended from the next side. interior exterior angles. another example: interior exterior .

The sum of the measures of the interior angles of a polygon with n sides is (n 2)180.. the measure of each interior angle of an equiangular n-gon is. if you count one exterior angle at each vertex, the sum of the measures of the exterior angles of a polygon is relationship between exterior and interior angles of a polygon always 360°. An exterior angle is the angle between any side of the polygon and a line extended from the next side. here is an example to help. if you draw an triangle, the angles inside it are interior angles.

All the exterior angles of a polygon add up to 360°, so: each exterior angle must be 360°/n interior angle = 180° − exterior angle. we know the exterior angle = 360°/n, so: there are a lot more relationships like those (most of them just "re-arrangements"), but those will do for now. Polygons also have interior and exterior angles. as we see in the diagram below, for all convex polygons, the sum of an interior and exterior angle is 180˚ making them supplementary angles. if you recall from integrated math 1, since these angles share a common side we can also classify them as a linear pair. Calculating the exterior angles of regular polygons · the sum of interior angles in a triangle is 180°. · all the interior angles in a regular polygon are equal. · the sum . An interior angle of a polygon is always supplementary to an exterior angle at its vertex, therefore they would add up to 180 degrees. equation. a quick way to find  .

Geometry: polygons: properties of polygons sparknotes.

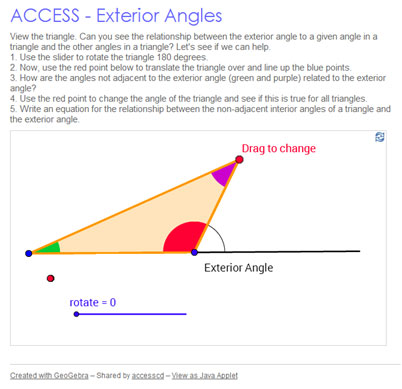
Refer to the figure above. it shows in detail one vertex of the polygon. you can see that the interior angle and exterior angle are supplementary, adding to 180°. as you drag the vertex downwards the polygon becomes concave, with the vertex pushed inwards towards the center of the polygon. as this happens the extended side now moves inside the polygon and the exterior angle becomes negative. Relationship of exterior / interior angles of a polygon. the interior angle is always supplementary to an exterior angle at that vertex. try this adjust the polygon . Interiorangle is 4x. a) use the relationship between interior and exterior angles to find x. b) find the measure of one interior and exterior angle. c) find the number of sides in the polygon and the type of polygon. 4) the measure of one interior angle of a regular polygon is 144°. how many sides does it have?. An interior angle and the corresponding exterior angle add up to a straight angle. that is, they are supplementary.

Each interior angle of a regular polygon is 18 degree more than eight times an exterior angle. the number os sides of polygon is. math please helppp 1 find the missing angle measure in the polygon a ] 77 b ] 87 c ] 97 d ] 107 i think its b 2 find the sum of the interior angles in 10 sided polygon a ] 1,260 b ] 1,440 c ] 1,620 relationship between exterior and interior angles of a polygon d ] 1,800 i. Use the geogebra applet below to explore the relationship between the number of sides of a polygon and the interior and exterior angles of that polygon. you can move the points in the polygons, but be sure to keep the polygon convex! fill in the spreadsheet on the right with the number of sides of.

Interior angles of polygons. an interior angle is an angle inside a shape. interior exterior angles. another example: interior exterior angles . Well, i would assume that we are talking about a regular polygon (all sides equal). then the central angle = 360/n, where n is the number of sides. the interior angles of a polygon add up to 180(n-2) therefore each interior angle is 180(n-2)/n. the exterior angles of a polygon add up relationship between exterior and interior angles of a polygon to 360, so 360/n. so central/exterior = 1. Properties. the sum of the internal angle and the external angle on the same vertex is 180°. the sum of all the internal angles of a simple polygon is 180(n–2)° where n is the number of sides. the formula can be proved using mathematical induction and starting with a triangle for which the angle sum is 180°, then replacing one side with two sides connected at a vertex, and so on. What is the relation between the sides and the angles of a regular polygon? 1. there will be as many angles as the number of sides (n). 2. each exterior angle will be equal to 360/n. 3. each interior angle will be equal to (180-360/n). 4. there wi.